Other posts in series
The algorithm
In my last post, I said I wanted to code up an alpha-beta pruning algorithm. (See this CS50 Intro to AI lecture for background on tree-based search and alpha-beta pruning). Over the past couple of weeks, I have been thinking about exactly how the algorithm would work and how I would code it up, and it was surprisingly tricky. I therefore decided to just focus on creating an algorithm that would search through a game-tree up to some maximum depth, but in a way that I could add in the pruning.
The algorithm should determine the ‘value’ of the current board state and the move that would achieve that value. A value of 1 means that Player 1 will win (with perfect play) and a value of 0 means that Player 0 will win (with perfect play). A value in the middle indicates which player is more likely to win, as judged by the algorithm.
The general idea of the algorithm is straightforward:
- Given a board position, create an initial node and add it to the frontier.
- While the initial node does not have a value, pick a node from the frontier and do the following:
- Check if the game has ended. If so, determine who won, and set the value of the node appropriately. Then update the value of parent nodes appropriately.
- Check if the depth of the node is the maximum depth. If so, then estimate the value of the position. For now, I just set this as 0.5, but in future, this will be determined via a neural network. Then update the value of parent nodes appropriately.
- Create a list of legal moves and possible board positions arising from this node. Create new nodes and add them to the frontier.
- Once the initial node has a value, pick a move whose resulting board position has the same value.
The tricky part was the step ‘update the value of the parent nodes appropriately’. It took me some time to flesh out all the details and determine exactly when a parent node should have its value updated. I had to do this in a way so that I could add on the pruning later without having to change the structure of the code. The main ideas were:
-
Whenever a node has its value determined, the upper or lower bounds of its parent’s node, and only its parent’s node, needs to be updated.
-
Whenever all of a node’s children’s values are determined, the node’s value can be determined. This will sometimes lead to some recursive updating of node values.
A big sticking point for me was how to decide when to prune a node: it felt like I needed knowledge of uncle/aunt nodes to do this, but following the ideas above, the grandparent node and parent node should contain enough information to decide if a node can be pruned or not.
In the end, I managed to get it altogether. The code, at this stage of the project, can be found on github.
An example
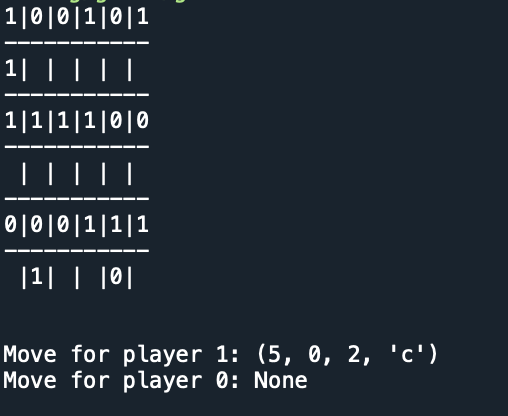
The image above shows an example winning position for player 1. If it is Player 1’s move, the algorithm finds a winning move using a depth-1 search (play in bottom left, and then rotate bottom left clockwise, giving 5-in-a-row column on left-hand-side). If it is Player 2’s move, the algorithm returns None using a depth-2 search, because no matter what 2 does on this turn, 1 will always win.
The code
The code, at this stage of project, can be found on github.
Areas of improvement
The algorithm is highly inefficient. It takes roughly 10-50 seconds to do depth-2 searches, and on the order of hours for depth-3 search. This is way too long! The number of possible positions after 3 moves is roughly a few million, so that shouldn’t take hours to sort through.
There are many inefficiencies I am aware of and will fix them for my next post. Examples include:
- Dealing with repeat positions. Right now, I only avoid positions that repeat if they arise from the same parent.
- I currently use a list to track which positions have been visited in the search, to check for repeats. This is less efficient than a set, but I can’t use arrays in sets and all my boards are coded as arrays. I will try changing everything to tuples.
- If a winning/losing sequence is found, it will keep on searching. This is not necessarily a bad thing, because we might want to analyse all the lines, but it definitely slows things down.
- Not using alpha-beta pruning, yet.
- Not doing any time analysis. I will run cProfile to systematically find inefficiencies.