- Other posts in series
- Performance before any optimisations
- The optimisations
- Next steps and final thoughts
- The code
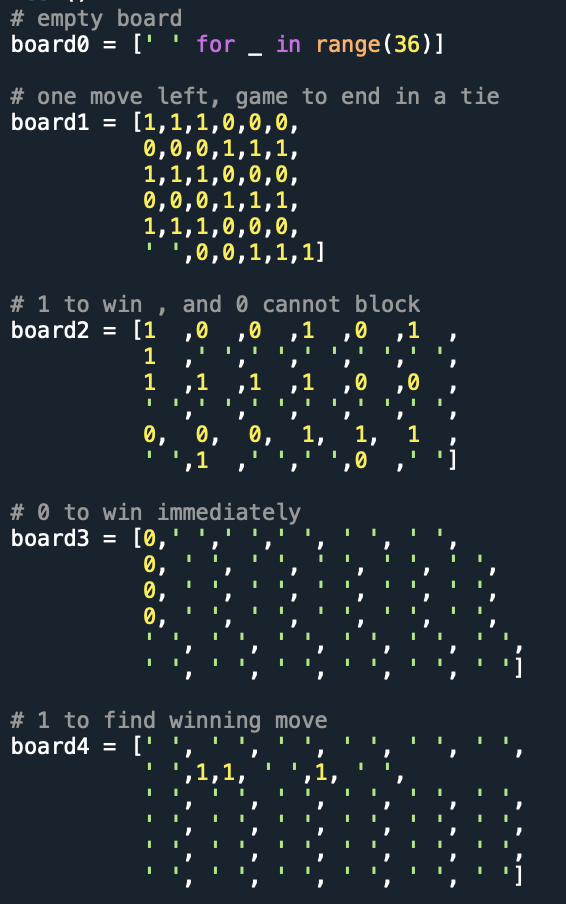
- The boards used for testing
Other posts in series
Performance before any optimisations
I created a few boards and timed how long it took the algorithm to run a depth-2 search on these boards, starting with both Player 0 and Player 1. An image showing the boards used is at the end of the post. The results are:
- Board: 0, Player: 0, Time taken: 1.59
- Board: 0, Player: 1, Time taken: 1.58
- Board: 1, Player: 0, Time taken: 0.00117
- Board: 1, Player: 1, Time taken: 0.00103
- Board: 2, Player: 0, Time taken: 5.04
- Board: 2, Player: 1, Time taken: 4.94
- Board: 3, Player: 0, Time taken: 29.2
- Board: 3, Player: 1, Time taken: 32.0
- Board: 4, Player: 0, Time taken: 9.55
- Board: 4, Player: 1, Time taken: 9.25
I also tried running a depth-3 search on Board 4 for Player 1 (because Player 1 can find a winning move with this depth), but it did not finish running even after a couple of hours of running.
The optimisations
I made several optimisations. I describe them here chronologically, i.e., in the order I tried implementing them.
Alpha-beta pruning
There are situations where a board position does not need to be analysed, because based on the boards we have already analysed, this board position will definitely not be chosen in optimal player. This resulted in the following times:
- Board: 0, Player: 0, Time taken: 1.34
- Board: 0, Player: 1, Time taken: 1.39
- Board: 1, Player: 0, Time taken: 0.00120
- Board: 1, Player: 1, Time taken: 0.00104
- Board: 2, Player: 0, Time taken: 5.28
- Board: 2, Player: 1, Time taken: 4.61
- Board: 3, Player: 0, Time taken: 26.1
- Board: 3, Player: 1, Time taken: 29.4
- Board: 4, Player: 0, Time taken: 8.62
- Board: 4, Player: 1, Time taken: 8.28
This was not a significant improvement in the times. I was surprised by this. I decided to run cProfile to try to determine why there was not a significant time-save. It seemed to be that the process of creating new boards was taking up a lot of time - and I was only pruning a board after the board was created. I needed to prune before the board was created.
To achieve this, I had to significantly re-structure the whole program, removing the frontier and instead writing the main function find_move recursively. The resulting times were a significant improvement:
- Board: 0, Player: 0, Time taken: 1.07
- Board: 0, Player: 1, Time taken: 1.06
- Board: 1, Player: 0, Time taken: 0.00118
- Board: 1, Player: 1, Time taken: 0.00102
- Board: 2, Player: 0, Time taken: 1.90
- Board: 2, Player: 1, Time taken: 1.86
- Board: 3, Player: 0, Time taken: 5.33
- Board: 3, Player: 1, Time taken: 5.41
- Board: 4, Player: 0, Time taken: 2.98
- Board: 4, Player: 1, Time taken: 2.90
Phew! It was satisfying to see the times drop so much, and this motivated me to keep going.
Stop if winning move found
If a winning move was found in a current board position, there is no need to continue analysing this position, so can stop this early. Pruning does not detect this (at least, not how I implemented it. This could be a sign I did it wrong…), so I had to manually add this. This resulted in further improvements:
- Board: 0, Player: 0, Time taken: 1.09
- Board: 0, Player: 1, Time taken: 1.11
- Board: 1, Player: 0, Time taken: 0.00104
- Board: 1, Player: 1, Time taken: 0.00119
- Board: 2, Player: 0, Time taken: 0.324
- Board: 2, Player: 1, Time taken: 0.344
- Board: 3, Player: 0, Time taken: 0.141
- Board: 3, Player: 1, Time taken: 0.897
- Board: 4, Player: 0, Time taken: 3.12
- Board: 4, Player: 1, Time taken: 2.93
I also tried running the depth-3 search on board 4, and to my surprise it ended in under a minute!
- Board: 4, Depth 3, Time taken: 59.1
Note this would not be representative of a generic depth-3 search, because the winning move is found about 1/6 of the way into the full search.
Lists within lists
Running cProfile revealed that having nested lists to encode the board slows things down considerably, so I re-wrote the program so that the board was represented by a single list. I was worried this would take a lot of effort, but fortunately it consisted of replacing board[i][j] with board[6*i + j], and other similar simple changes. This halved the times:
- Board: 0, Player: 0, Time taken: 0.407
- Board: 0, Player: 1, Time taken: 0.411
- Board: 1, Player: 0, Time taken: 0.000520
- Board: 1, Player: 1, Time taken: 0.000450
- Board: 2, Player: 0, Time taken: 0.175
- Board: 2, Player: 1, Time taken: 0.161
- Board: 3, Player: 0, Time taken: 0.0645
- Board: 3, Player: 1, Time taken: 0.424
- Board: 4, Player: 0, Time taken: 1.41
- Board: 4, Player: 1, Time taken: 1.41
- Board: 4, Depth 3, Time taken: 30.7
Checking if the game is over
Running cProfile again showed that the new bottle-neck was checking if the game had ended. This involved looping through the set of all possible winning lines, and checking to see if Player 0 or Player 1 occupied all the positions in each line.
Originally, I had one for-loop to check if Player 1 won, then another to check if Player 0 won. I changed this to have a single loop, and for each line check if Player 1 or Player 0 won. This resulted in another big chunk of time-saving.
- Board: 0, Player: 0, Time taken: 0.292
- Board: 0, Player: 1, Time taken: 0.283
- Board: 1, Player: 0, Time taken: 0.000499
- Board: 1, Player: 1, Time taken: 0.000334
- Board: 2, Player: 0, Time taken: 0.101
- Board: 2, Player: 1, Time taken: 0.107
- Board: 3, Player: 0, Time taken: 0.0359
- Board: 3, Player: 1, Time taken: 0.261
- Board: 4, Player: 0, Time taken: 0.943
- Board: 4, Player: 1, Time taken: 0.915
- Board: 4, Depth 3, Time taken: 21.6
Checking cProfile showed that I had halved the time to check if the game had ended, but it was still the biggest bottle neck.
I then tried to re-design the program to cut down further, but to no avail. For example, I tried to group the set of lines into groups that could be ruled out together, e.g. if I know that position (2,2) in the board is empty, that rules out 7 of the lines. It will be interesting to know if there is a more efficient way to check if the game has ended!
Tidying up and fixing a “bug”
My code was becoming untidy (I was not using version control properly, and instead was creating multiple versions of functions in the same file) so I tidied up all the code. While doing this, I discovered that I did not correctly update the prune function during the ‘Lists within lists’ step: I was only pruning boards of at least depth 2, when it could be pruning board of depth 1. I made the necessary tweak, resulting in the following times:
- Board: 0, Player: 0, Time taken: 0.0896
- Board: 0, Player: 1, Time taken: 0.0682
- Board: 1, Player: 0, Time taken: 0.000272
- Board: 1, Player: 1, Time taken: 0.000204
- Board: 2, Player: 0, Time taken: 0.100
- Board: 2, Player: 1, Time taken: 0.0539
- Board: 3, Player: 0, Time taken: 0.313
- Board: 3, Player: 1, Time taken: 1.13
- Board: 4, Player: 0, Time taken: 0.204
- Board: 4, Player: 1, Time taken: 0.310
- Board: 4, Depth 3, Time taken: 3.18
Woohoo! What big progress. What used to take hours now only takes 3 seconds.
Duplicate board positions
The last thing I wanted to try was dealing with repeat positions. Previously I only skipped these if the same position occurred and they had same parent. But now I wanted to have a way of skipping board positions regardless of where they were in the game-tree. This took many hours to get correct, because my first attempt caused the algorithm to produce sub-optimal moves, and I had no idea why.
The error was that when I pruned a board, I would finalise the board’s value, though the board was not fully analysed. Then, when the board occurred somewhere else in the tree, I would use this incomplete value and miss out all the analysis that was pruned the first time around.
After fixing the bug, the new times are:
- Board: 0, Player: 0, Time taken: 0.2888009548187256
- Board: 0, Player: 1, Time taken: 0.15045881271362305
- Board: 1, Player: 0, Time taken: 0.00028705596923828125
- Board: 1, Player: 1, Time taken: 0.0002300739288330078
- Board: 2, Player: 0, Time taken: 0.0822603702545166
- Board: 2, Player: 1, Time taken: 0.03888416290283203
- Board: 3, Player: 0, Time taken: 0.30017614364624023
- Board: 3, Player: 1, Time taken: 0.7593698501586914
- Board: 4, Player: 0, Time taken: 0.3503570556640625
- Board: 4, Player: 1, Time taken: 0.3380570411682129
- Board: 4, Depth 3, Time taken: 3.19
The times are not always better, and some are worse.
Next steps and final thoughts
The next step is to introduce neural networks. A brief google search reveals that min-max is not appropriate and that I should have been using reinforcement learning. Doh! In the back of my mind, I was curious as to how the neural network could learn the heuristic function; what would the loss/error be that it would minimise?
Though the optimisation of the min-max algorithm is incomplete (e.g. I do not understand why the latest version is not faster than the previous version), I will end it here. This is because I have already spent a couple of days on this, I have already learnt from this, and it is not necessary for the bigger goal of developing a neural network.
Some final takeaways:
- I should have sketched out a plan of the whole project. Though I had basic knowledge of neural networks, I should have researched a bit more and found out that min-max is not appropriate for neural networks.
- Be more thorough with testing. It makes spotting bugs easier and quicker.
- Seed random number generators. I used used random heuristics (to see effects of pruning), but I did not seed them. This means the times above are not fair comparisons, as some random numbers could have lead to more pruning than others.
- Use proper version control. My code got hideous at one point. At least now I have a better sense of the workflow of git.
The code
The code, at this stage of project, can be found on github.
The boards used for testing