- Other posts in series
- First attempt
- Second attempt
- Final thoughts
- Code for first attempt
- Code for second attempt
Other posts in series
First attempt
I used a k-fold cross validation with 4 folds to determine what is a good number of estimators for the Random Forest model. The code to do this is at the bottom. The table below shows the AUC metrics obtained.
| Fold | n_estimators = 10 | n_estimators = 50 | n_estimators = 100 | n_estimators = 200 | n_estimators = 500 |
|---|---|---|---|---|---|
| 0 | 0.765 | 0.793 | 0.775 | 0.770 | 0.756 |
| 1 | 0.683 | 0.690 | 0.691 | 0.680 | 0.664 |
| 2 | 0.766 | 0.783 | 0.781 | 0.784 | 0.774 |
| 3 | 0.815 | 0.841 | 0.838 | 0.833 | 0.826 |
From this table, we can see that the AUC depends a lot more on the fold rather than the hyper-parameter. I was surprised at how much the AUC could vary, depending on how the data was chopped up. Nevertheless, it is still clear that the optimal choice for the number of estimators is either 50 or 100. However, it is hard to judge if 50 is definitely better than the default of 100; it is better in 3 out of the 4 folds but maybe this was just a fluke.
I wanted to better understand how the AUC depends on the folds, and make a better decision about which hyper-parameter is better, so I decided to repeat this process many times and see the resulting patterns.
Second attempt
I repeated the first attempt 20 times and stored the results in a pandas dataframe. I then plotted scatterplots and histograms to visualise the patterns. In each of them, I compared the performance against the default of 100 estimators. As always, the code for this is at the bottom.
n_estimators=10
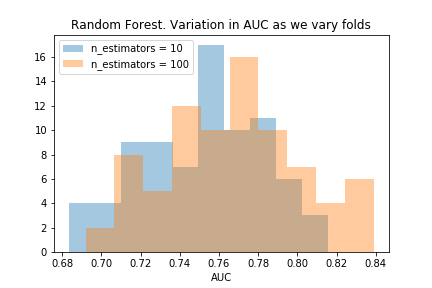
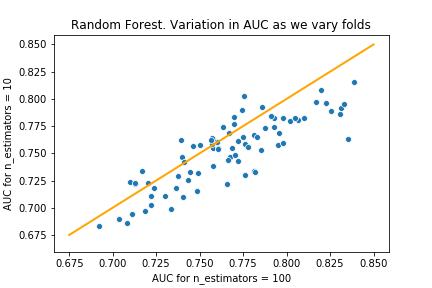
The histogram shows that the distribution of AUC values when the number of estimators is 10 is worse than the default values. The scatterplot shows the default setting has a better AUC on the majority of folds - but not every time!
n_estimators=50
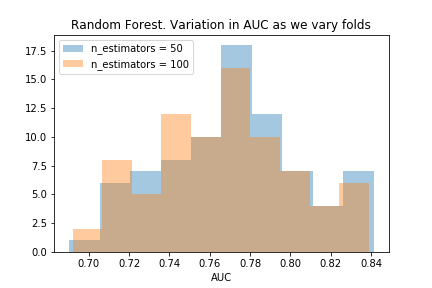
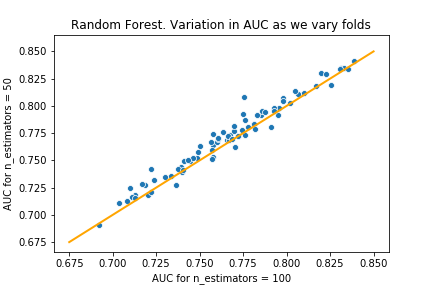
The histograms almost perfectly overlap! But we do see a little extra blue on the right and extra orange on the left which means n=50 is better. The scatterplot makes this clearer, showing that having 50 estimators produces larger AUC in most of the folds.
n_estimators=200 and n_estimators=500
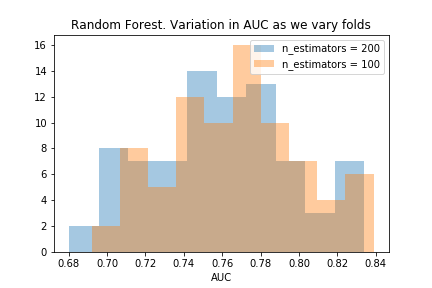
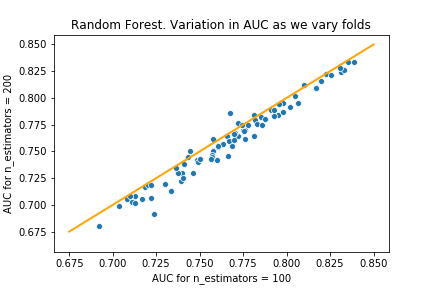
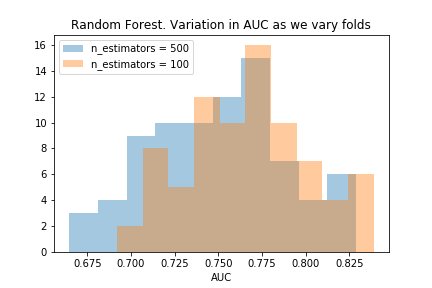
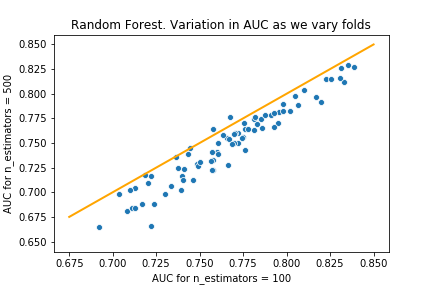
From these charts, we see that as we increase the number of estimators beyond 100, the model performs worse. Though we can see this in the table in the first attempt, these charts make it much clearer.
Final thoughts
Visualisations are nice! Though the first k-fold validation gave the same conclusions as twenty k-fold validations, the latter is far more convincing and enlightening. In addition to being more certain that n=50 is a superior choice, I have gained knowledge about how much the AUC can vary as the data varies.
Furthermore, the idea of removing data to speed up the fitting (from Part II of the series) really paid off. Generating these charts required 320 fittings altogether. Without removing the data, this would have taken multiple days, so I would never have done it.
Next time, I will complete the hyper-parameter optimisations and present my final models.
Code for first attempt
#create train-valid versus test split
Xtv, X_test, ytv, y_test = train_test_split(X,y, random_state=0, test_size=0.2)
#create KFold object
kf = KFold(n_splits = 4,
shuffle = True,
random_state = 0)
#create function to determine auc given the data
def auc_model(model, Xt, Xv, yt, yv):
model.fit(Xt,yt)
preds = model.predict_proba(Xv)
preds = preds[:,1]
precision, recall, _ = precision_recall_curve(yv, preds)
auc_current = auc(recall, precision)
return auc_current
# create list of n_estimators for RandomForest
n_estimators = [10, 50, 100, 200, 500]
# create variable to store aucs
aucs = np.zeros([5,4])
# loop through hyper-parameter values and folds
i=0
for n_estimator in n_estimators:
j = 0
model = RandomForestClassifier(n_estimators = n_estimator,
random_state = 0)
for train, valid in kf.split(Xtv):
Xt, Xv, yt, yv = Xtv.iloc[train], Xtv.iloc[valid], ytv.iloc[train], ytv.iloc[valid]
# remove 99% of the non-fraudulent claims from training data to speed up fitting
selection = (Xt.index % 100 == 1) | (yt == 1)
Xt_reduced = Xt[selection]
yt_reduced = yt[selection]
auc_current = auc_model(model, Xt_reduced, Xv, yt_reduced, yv)
aucs[i][j] = auc_current
j += 1
i += 1
Code for second attempt
# create list of n_estimators for RandomForest
n_estimators = [10, 50, 100, 200, 500]
# create variables to store auc data
aucs = np.zeros([5,4])
auc_df = pd.DataFrame({'n_estimators_'+str(n_estimators[i]): []
for i in range(len(n_estimators))})
# create 20 different KFolds, so we get 80 models for each value of hyperparameter
for random_state in range(20):
kf = KFold(n_splits = 4,
shuffle = True,
random_state = random_state)
i=0
for n_estimator in n_estimators:
j = 0
model = RandomForestClassifier(n_estimators = n_estimator,
random_state = 0)
for train, valid in kf.split(Xtv):
Xt, Xv, yt, yv = Xtv.iloc[train], Xtv.iloc[valid], ytv.iloc[train], ytv.iloc[valid]
# remove 99% of the non-fraudulent claims from training data to speed up fitting
selection = (Xt.index % 100 == 1) | (yt == 1)
Xt_reduced = Xt[selection]
yt_reduced = yt[selection]
auc_current = auc_model(model, Xt_reduced, Xv, yt_reduced, yv)
aucs[i][j] = auc_current
j += 1
i += 1
# update dataframe auc_df with latest batch of aucs
for j in range(4):
auc_df.loc[auc_df.shape[0]] = aucs[:,j]